In the previous topic, we learned that the Earth's seasons are controlled by changes in the duration and intensity of solar radiation or insolation. Both of these factors are in turn governed by the annual change in the position of the Earth's axis relative to the Sun (see Figure 6h-4).
Yearly changes in the position of the Earth's axis cause the location of the Sun to wander 47° across our skies. Changes in the location of the Sun have a direct effect on the intensity of solar radiation. The intensity of solar radiation is largely a function of the angle of incidence, the angle at which the Sun's rays strike the Earth's surface. If the Sun is positioned directly overhead or 90° from the horizon, the incoming insolation strikes the surface of the Earth at right angles and is most intense. If the Sun is 45° above the horizon, the incoming insolation strikes the Earth's surface at an angle. This causes the rays to be spread out over a larger surface area reducing the intensity of the radiation. Figure 6i-1 models the effect of changing the angle of incidence from 90 to 45°. As illustrated, the lower Sun angle (45°) causes the radiation to be received over a much larger surface area. This surface area is approximately 40% greater than the area covered by an angle of 90°. The lower angle also reduces the intensity of the incoming rays by 30%.
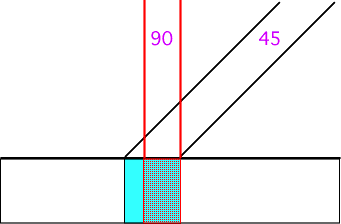
Figure 6i-1: Effect of angle on the area that intercepts an incoming beam of radiation.
We can also model the effect the angle of incidence has on insolation intensity with the following simple equation:
Intensity = SIN (A)
where, A is the angle of incidence and SIN is the sine function found on most calculators. Using this equation we can determine that an angle of 90° gives us a value of 1.00 or 100% (1.00 x 100). Let us compare this maximum value with values determined for other angles of incidence. Note the answers are expressed as a percentage of the potential maximum value.
SIN 80 = 0.98 or 98%
SIN 70 = 0.94 or 94%
SIN 60 = 0.87 or 87%
SIN 50 = 0.77 or 77%
SIN 40 = 0.64 or 64%
SIN 30 = 0.50 or 50%
SIN 20 = 0.34 or 34%
SIN 10 = 0.17 or 17%
SIN 0 = 0.00 or 0%
The yearly changes in the position of the Earth's axis relative to the plane of the ecliptic also causes seasonal variations in day length to all locations outside of the equator. Longest days occur during the June solstice for locations north of the equator and on the December solstice for locations in the Southern Hemisphere. The equator experiences equal day and night on every day of the year. Day and night is also of equal length for all Earth locations on the September and March equinoxes. Figure 6i-2 describes the change in the length of day for locations at the equator, 10, 30, 50, 60, and 70 degrees North over a one-year period. The illustration suggests that days are longer than nights in the Northern Hemisphere from the March equinox to the September equinox. Between the September to March equinox days are shorter than nights in the Northern Hemisphere. The opposite is true in the Southern Hemisphere. The graph also shows that the seasonal (winter to summer) variation in day length increases with increasing latitude.
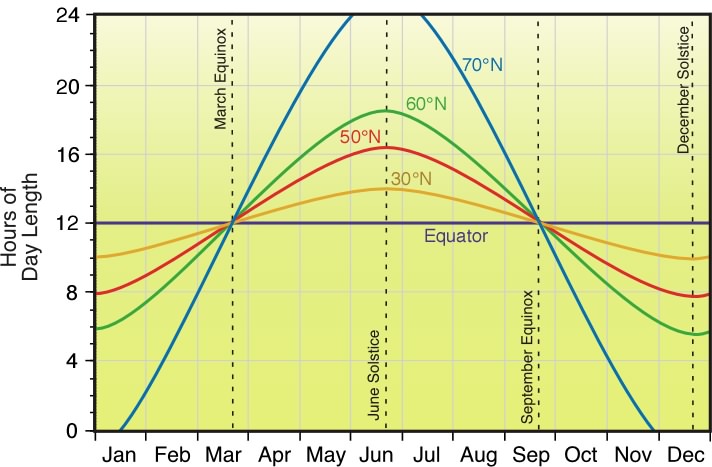
| Figure 6i-2: Annual variations in day length for locations at the equator, 30, 50, 60, and 70° North latitude. |
Figure 6i-3 below describes the potential insolation available for the equator and several locations in the Northern Hemisphere over a one-year period. The values plotted on this graph take into account the combined effects of angle of incidence and day length duration (see Table 6h-2). Locations at the equator show the least amount of variation in insolation over a one-year period. These slight changes in insolation result only from the annual changes in the altitude of the Sun above the horizon, as the duration of daylight at the equator is always 12 hours. The peaks in insolation intensity correspond to the two equinoxes when the Sun is directly overhead. The two annual minimums of insolation occur on the solstices when the maximum height of the Sun above the horizon reaches an angle of 66.5°.
The most extreme variations in insolation received in the Northern Hemisphere occur at 90 degrees North. During the June solstice this location receives more potential incoming solar radiation than any other location graphed. At this time the Sun never sets. In fact, it remains at an altitude of 23.5 degrees above the horizon for the whole day. From September 22 (September equinox) to March 21, (March equinox) no insolation is received at 90 degrees North. During this period the Sun slips below the horizon as the northern axis of the Earth has an orientation that is tilted away from the Sun.
The annual insolation curve for locations at 60 degrees North best approximates the seasonal changes in solar radiation intensity perceived at our latitude. Maximum values of insolation are received at the June solstice when day length and angle of incidence are at their maximum (see Table 6h-2 and section 6h). During the June solstice day length is 18 hours and 27 minutes and the angle of the Sun reaches a maximum value of 53.5 degrees above the horizon. Minimum values of insolation are received during the December solstice when day length and angle of incidence are at their minimum (see Table 6h-2 and section 6h). During the December solstice day length is only 5 hours and 33 minutes and the angle of the Sun reaches a lowest value of 6.5 degrees above the horizon.
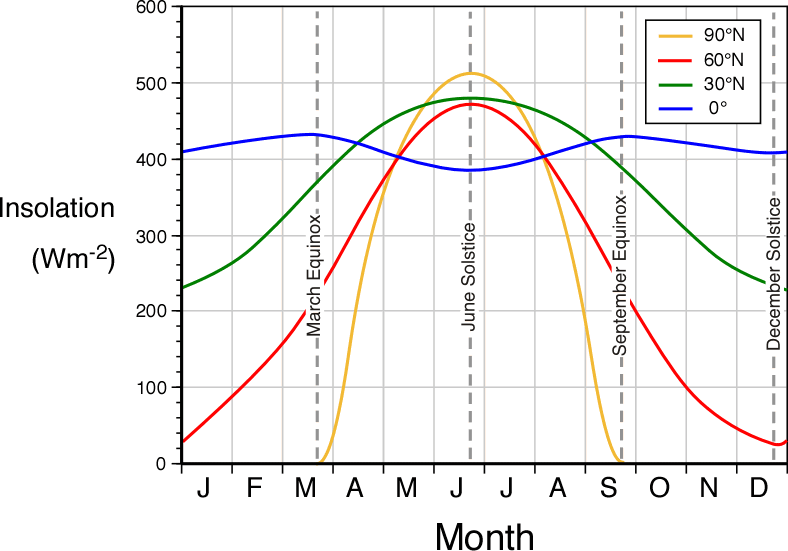
Figure 6i-3: Monthly values of available insolation in Wm-2 for the equator, 30, 60, and 90° North.