Introduction
Wind can be defined simply as air in motion. This motion can be in any direction, but in most cases the horizontal component of wind flow greatly exceeds the flow that occurs vertically. The speed of wind varies from absolute calm to speeds as high as 380 kilometers per hour (Mt. Washington, New Hampshire, April 12, 1934). In 1894, strong winds in Nebraska pushed six fully loaded coal cars over 160 kilometers in just over three hours. Over short periods of time surface winds can be quite variable.
Wind develops as a result of spatial differences in atmospheric pressure. Generally, these differences occur because of uneven absorption of solar radiation at the Earth's surface (Figure 7n-1). Wind speed tends to be at its greatest during the daytime when the greatest spatial extremes in atmospheric temperature and pressure exist.
Figure 7n-1: Formation of wind as a result of localized temperature differences.
Wind is often described by two characteristics: wind speed and wind direction. Wind speed is the velocity attained by a mass of air traveling horizontally through the atmosphere. Wind speed is often measured with an anemometer in kilometers per hour (kmph), miles per hour (mph), knots, or meters per second (mps) (Figure 7n-2). Wind direction is measured as the direction from where a wind comes from. For example, a southerly wind comes from the south and blows to the north. Direction is measured by an instrument called a wind vane (Figure 7n-2). Both of these instruments are positioned in the atmospheric environment at a standard distance of 10 meters above the ground surface.
Wind speed can also be measured without the aid of instruments using the Beaufort wind scale (Table 7n-1). This descriptive scale was originally developed by Admiral Beaufort of the British Navy in the first decade of the 17th century. The purpose for this system was to allow mariners to determine wind speed from simple observations. The Beaufort system has undergone several modifications to standardize its measurement scale and to allow for its use on land. Users of this scale look for specific effects of the wind on the environment to determine speed.

|
Figure
7n-2: Meteorological
instruments used to measure wind speed and
direction. Wind speed is commonly measured
with an anemometer.
An anemometer consists of three open cups attached
to a rotating spindle. The speed of roation
is then converted into a measurement of wind
speed. Wind direction is measured with a wind vane.
On the photograph above, the wind vane instrument
has a bullet shaped nose attached to a finned
tail by a metal bar. |
Table 7n-1: Beaufort wind speed scale.
|
Beaufort Code |
Speed Miles per Hour |
Speed Kilometers per Hour |
Description |
Effects on the Environment |
|
0 |
< 1 |
< 1 |
calm |
smoke rises vertically |
|
1 |
2 - 3 |
1 - 5 |
light air |
smoke drifts slowly |
|
2 |
4 - 7 |
6 - 11 |
light breeze |
leaves rustle, wind can be felt, wind vanes move |
|
3 |
8 - 12 |
12 - 19 |
gentle breeze |
leaves and twigs on trees move |
|
4 |
13 - 18 |
20 - 29 |
moderate breeze |
small tree branches move, dust is picked up from the ground surface |
|
5 |
19 - 24 |
30 - 38 |
fresh breeze |
small trees move |
|
6 |
25 - 31 |
39 - 51 |
strong breeze |
large branches move, telephone and power overhead wires whistle |
|
7 |
32 - 38 |
51 - 61 |
near gale |
trees move, difficult to walk in the wind |
|
8 |
39 - 46 |
62 - 74 |
gale |
twigs break off from trees |
|
9 |
47 - 54 |
75 - 86 |
strong gale |
branches break off from trees, shingles blown off roofs |
|
10 |
55 - 63 |
87 - 101 |
whole gale |
trees become uprooted, structural damage on buildings |
|
11 |
64 - 74 |
102 - 120 |
storm |
widespread damage to buildings and trees |
|
12 |
> 75 |
> 120 |
hurricane |
severe damage to buildings and trees |
Winds are named according to the compass direction of their source. Thus, a wind from the north blowing toward the south is called a northerly wind. Figure 7n-3 describes the sixteen principal bearings of wind direction. Most meterological observations report wind direction using one of these sixteen bearings.
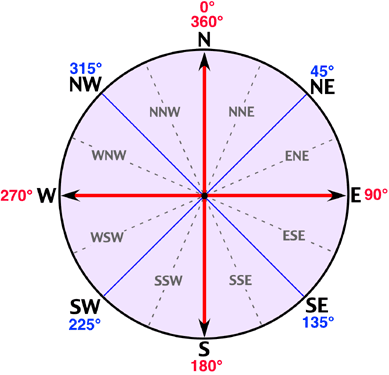
|
Figure
7n-3: Wind
compass describing the sixteen principal bearings
used to measure wind direction. This compass
is based on the 360 degrees found in a circle. |
Horizontally, at the Earth's surface wind always blows from areas of high pressure to areas of low pressure (vertically, winds move from areas of low pressure to areas of high pressure), usually at speeds determined by the rate of air pressure change between pressure centers. This situation is comparable to someone skiing down a hill. The skier will of course move from the top of the hill to the bottom of the hill, with the speed of their descent controlled by the gradient or steepness of the slope. Likewise, wind speed is a function of the steepness or gradient of atmospheric air pressure found between high and low pressure systems. When expressed scientifically, pressure change over a unit distance is called pressure gradient force, and the greater this force the faster the winds will blow.
On weather maps, pressure is indicated by drawing isolines of pressure, called isobars, at regular 4 millibar intervals (e.g., 996 mb, 1000 mb, 1004 mb, etc.). If the isobars are closely spaced, we can expect the pressure gradient force to be great, and wind speed to be high (see Figure 7n-4). In areas where the isobars are spaced widely apart, the pressure gradient is low and light winds normally exist. High speed winds develop in areas where isobars are closer.
|
Figure
7n-4: Association
between wind speed and distance between isobars.
In the illustration above thicker arrows
represent relatively faster winds. |
Driving Forces
To better understand wind we must recognize that it is the result of a limited number of accelerating and decelerating forces, and that the action of these forces is controlled by specific fundamental natural laws. Sir Isaac Newton formulated these laws as several laws of motion. The first law suggests that an object that is stationary will remain stationary, and an object in motion will stay in motion as long as no opposing force is put on the object. As a result of this law, a puck sent in flight from a blade of a hockey stick will remain in motion until friction slows it down or the goalie makes a save. This law also suggests that once in motion an object's path should be straight.
Newton's second law of motion suggests that the force put on an object equals its mass multiplied by the acceleration produced. The term force in this law refers to the total or net effect of all the forces acting on an object. Mathematically, this law is written as:
Force = Mass x Acceleration
or
Acceleration = Force/Mass
From this natural law of motion we can see that the acceleration of an object is directly proportional to the net force pushing or pulling that body and inversely proportional to the mass of the body. Thus, the greater the force created by the movement of a hockey player's stick the faster the puck will travel. This law also suggests that if the player used a larger (more massive) puck more force would have to be applied to it to get it to travel as fast as a puck with less mass.
In the previous lecture we briefly examined one of the forces, pressure gradient force, acting on wind. Let us return to this force and examine it in greater detail and in relation to Newton's laws of motion. We will also examine the effects of three other forces that act on air in motion.
Pressure gradient force is the primary force influencing the formation of wind from local to global scales. This force is determined by the spatial pattern of atmospheric pressure at any given moment in time. Figure 7n-5 illustrates two different pressure gradient scenarios and their relative effect on wind speed.
Figure 7n-5: Effect of pressure gradient on wind speed.
The two diagrams display the relative relationship
between pressure gradient and wind speed. This relationship
is linear and positive. As a result, quadrupling the
pressure gradient increases wind speed by a factor of
four. This is what we would expect according to Newton's
second law of motion, assuming the mass of the wind is
unchanged.
We can also describe pressure gradient acceleration mathematically with the following equation:
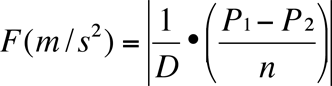
where:
D = density of air (average density of surface air is 1.29 kilograms per cubic meter)
P2 = pressure at point 2 in Newtons/m2 (N m-2)
P1 = pressure at point 1 in Newtons/m2 (N m-2)
n = distance between the two points in meters
From this equation we can determine wind acceleration between two points in meters per second squared by knowing three variables: the density of the moving air; the change in pressure between the points of interest in newtons; and the distance between the two points in meters. For example, to determine the wind speed between two points for moving air with a density of 1.29 kilograms per cubic meter, a pressure difference of 400 Newtons/m2, and a distance of 300,000 meters, the following calculations would be performed:
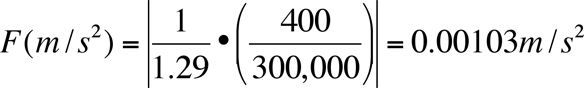
From the calculated value of acceleration we can determine wind speed, V, from the formula:
V = V0 + Ft
Where V0 is the initial velocity of the wind and t is the time during which F is applied.
The rotation of the Earth creates another force, termed Coriolis force, which acts upon wind and other objects in motion in very predictable ways. According to Newton's first law of motion, air will remain moving in a straight line unless it is influenced by an unbalancing force. The consequence of Coriolis force opposing pressure gradient acceleration is that the moving air changes direction. Instead of wind blowing directly from high to low pressure, the rotation of the Earth causes wind to be deflected off course. In the Northern Hemisphere, wind is deflected to the right of its path, while in the Southern Hemisphere it is deflected to the left. The magnitude of the Coriolis force varies with the velocity and the latitude of the object (see Figure 7n-6). Coriolis force is absent at the equator, and its strength increases as one approaches either pole. Furthermore, an increase in wind speed also results in a stronger Coriolis force, and thus in greater deflection of the wind. Coriolis force only acts on air when it has been sent into motion by pressure gradient force. Finally, Coriolis force only influences wind direction and never wind speed.
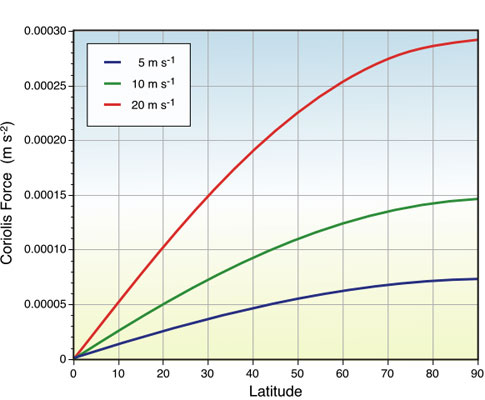
| Figure 7n-6: The strength of Coriolis force is influenced by latitude and the speed of the moving object. |
Centripetal acceleration is the third force that can act on moving air. It acts only on air that is flowing around centers of circulation. Centripetal acceleration is also another force that can influence the direction of wind. Centripetal acceleration creates a force directed at right angles to the flow of the wind and inwards towards the centers of rotation (e.g., low and high pressure centers). This force produces a circular pattern of flow around centers of high and low pressure. Centripetal acceleration is much more important for circulations smaller than the mid-latitude cyclone.
The last force that can influence moving air is frictional deceleration. Friction can exert an influence on wind only after the air is in motion. Frictional drag acts in a direction opposite to the path of motion causing the moving air to decelerate (see Newton's first and second laws of motion). Frictional effects are limited to the lower one kilometer above the Earth's surface.
Geostrophic Wind
Air under the influence of both the pressure gradient force and Coriolis force tends to move parallel to isobars in conditions where friction is low (1000 meters above the surface of the Earth) and isobars are straight. Winds of this type are usually called geostrophic winds. Geostrophic winds come about because pressure gradient force and Coriolis force come into balance after the air begins to move (Figure 7n-7).
|
Figure
7n-7: A
geostrophic wind flows parallel to the isobars.
In this model of wind flow in the Northern
Hemisphere, wind begins as a flow of air
perpendicular to the isobars (measured in millibars)
under the primary influence of the pressure
gradient force (PGF).
As the movement begins, the Coriolis force
(CF)
begins to influence the moving air causing
it to deflect to the right of its path. This
deflection continues until the pressure gradient
force and Coriolis force are opposite and
in balance with each other. |
Figure 7n-7 models air flow in the Northern Hemisphere. In the Southern Hemisphere, Coriolis acceleration acts on moving air by deflecting it to the left instead of the right.
Finally, Buy Ballot's Law states that when you stand with your back to a geostrophic wind in the Northern Hemisphere the center of low pressure will be to your left and the high pressure to your right. The opposite is true for the Southern Hemisphere.
Gradient Wind
Wind above the Earth's surface does not always travel in straight lines. In many cases winds flow around the curved isobars of a high (anticyclone) or low (cyclone) pressure center. A wind that blows around curved isobars above the level of friction is called a gradient wind. Gradient winds are slightly more complex than geostrophic winds because they include the action of yet another physical force. This force is known as centripetal force and it is always directed toward the center of rotation. The following figure describes the forces that produce gradient winds around high and low pressure centers (Figure 7n-8). Around a low, the gradient wind consists of the pressure gradient force and centripetal force acting toward the center of rotation, while Coriolis force acts away from the center of the low. In a high pressure center, the Coriolis and centripetal forces are directed toward the center of the high, while the pressure gradient force is directed outward.
| Figure 7n-8: The balance of forces that create a gradient wind in the Northern Hemisphere (PGF = pressure gradient force; CF = Coriolis force; Ce = centripetal force). In this diagram, CF = Ce + PGF for the low, and PGF = CF + Ce for the high. |
Friction Layer Wind
Surface winds on a weather map do not blow exactly parallel to the isobars as in geostrophic and gradient winds. Instead, surface winds tend to cross the isobars at an angle varying from 10 to 45°. Close to the Earth's surface, friction reduces the wind speed, which in turn reduces the Coriolis force. As a result, the reduced Coriolis force no longer balances the pressure gradient force, and the wind blows across the isobars toward or away from the pressure center. The pressure gradient force is now balanced by the sum of the frictional force and the Coriolis force. Thus, we find surface winds blowing counterclockwise and inward into a surface low, and clockwise and out of a surface high in the Northern Hemisphere. In the Southern Hemisphere, the Coriolis force acts to the left rather than the right. This causes the winds of the Southern Hemisphere to blow clockwise and inward around surface lows, and counterclockwise and outward around surface highs (see Figure 7n-9 below).
| Figure 7n-9: Circulation patterns of high and low pressure systems in the North and South Hemisphere. |