Location on Maps
Most maps allow us to specify the location of points on the Earth's surface using a coordinate system. For a two-dimensional map, this coordinate system can use simple geometric relationships between the perpendicular axes on a grid system to define spatial location. Figure 2b-1 illustrates how the location of a point can be defined on a coordinate system.
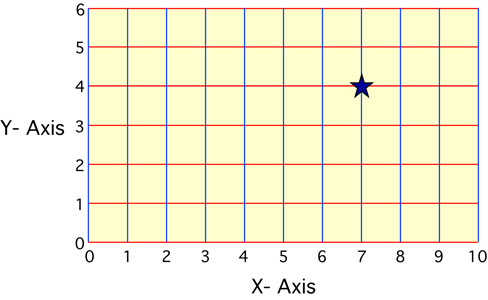
Figure 2b-1: A grid coordinate system defines the location of points from the distance traveled along two perpendicular axes from some stated origin. In the example above, the two axes are labeled X and Y. The origin is located in the lower left hand corner. Unit distance traveled along each axis from the origin is shown. In this coordinate system, the value associated with the X-axis is given first, following by the value assigned from the Y-axis. The location represented by the star has the coordinates 7 (X-axis), 4 (Y-axis). |
Two types of coordinate systems are currently in general use in geography: the geographical coordinate system and the rectangular (also called Cartesian) coordinate system.
Geographical Coordinate System
The geographical coordinate system measures location from only two values, despite the fact that the locations are described for a three-dimensional surface. The two values used to define location are both measured relative to the polar axis of the Earth. The two measures used in the geographic coordinate system are called latitude and longitude.
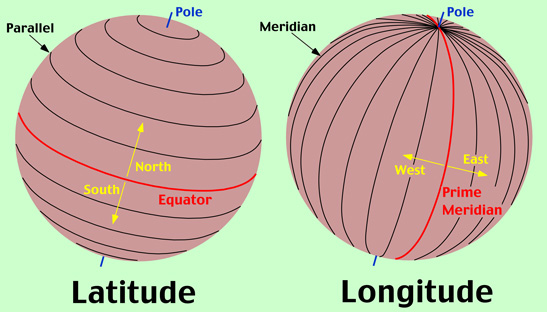
Figure 2b-2: Lines of latitude or parallels are drawn parallel to the equator (shown in red) as circles that span the Earth's surface. These parallels are measure in degrees (°). There are 90 angular degrees of latitude from the equator to each of the poles. The equator has an assigned value of 0°. Measurements of latitude are also defined as being either north or south of equator to distinguish the hemisphere of their location. Lines of longitude or meridians are circular arcs that meet at the poles. There are 180° of longitude either side of a starting meridian which is known the Prime Meridian. The Prime Meridian has a designated value of 0°. Measurements of longitude are also defined as being either west or east of the Prime Meridian. |
Latitude measures the north-south position of locations on the Earth's surface relative to a point found at the center of the Earth (Figure 2b-2). This central point is also located on the Earth's rotational or polar axis. The equator is the starting point for the measurement of latitude. The equator has a value of zero degrees. A line of latitude or parallel of 30° North has an angle that is 30° north of the plane represented by the equator (Figure 2b-3). The maximum value that latitude can attain is either 90° North or South. These lines of latitude run parallel to the rotational axis of the Earth.
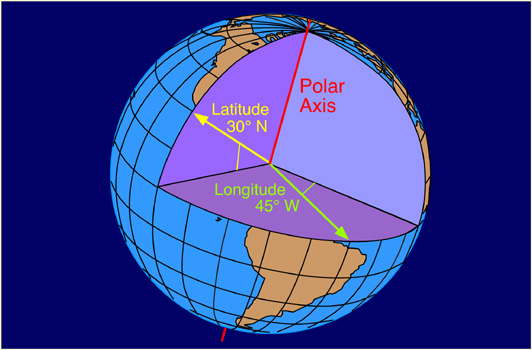
Figure 2b-3: Measurement of latitude and longitude relative to the equator and the Prime Meridian and the Earth's rotational or polar axis. |
Longitude measures the west-east position of locations on the Earth's surface relative to a circular arc called the Prime Meridian (Figure 2b-2). The position of the Prime Meridian was determined by international agreement to be in-line with the location of the former astronomical observatory at Greenwich, England. Because the Earth's circumference is similar to circle, it was decided to measure longitude in degrees. The number of degrees found in a circle is 360. The Prime Meridian has a value of zero degrees. A line of longitude or meridian of 45° West has an angle that is 45° west of the plane represented by the Prime Meridian (Figure 2b-3). The maximum value that a meridian of longitude can have is 180° which is the distance halfway around a circle. This meridian is called the International Date Line. Designations of west and east are used to distinguish where a location is found relative to the Prime Meridian. For example, all of the locations in North America have a longitude that is designated west.
Universal Transverse Mercator System (UTM)
Another commonly used method to describe location on the Earth is the Universal Transverse Mercator (UTM) grid system. This rectangular coordinate system is metric, incorporating the meter as its basic unit of measurement. UTM also uses the Transverse Mercator projection system to model the Earth's spherical surface onto a two-dimensional plane. The UTM system divides the world's surface into 60 - six degree longitude wide zones that run north-south (Figure 2b-5). These zones start at the International Date Line and are successively numbered in an eastward direction (Figure 2b-5). Each zone stretches from 84° North to 80° South (Figure 2b-4). In the center of each of these zones is a central meridian. Location is measured in these zones from a false origin which is determined relative to the intersection of the equator and the central meridian for each zone. For locations in the Northern Hemisphere, the false origin is 500,000 meters west of the central meridian on the equator. Coordinate measurements of location in the Northern Hemisphere using the UTM system are made relative to this point in meters in eastings (longitudinal distance) and northings (latitudinal distance). The point defined by the intersection of 50° North and 9° West would have a UTM coordinate of Zone 29, 500000 meters east (E), 5538630 meters north (N) (see Figures 2b-4 and 2b-5). In the Southern Hemisphere, the origin is 10,000,000 meters south and 500,000 meters west of the equator and central meridian, respectively. The location found at 50° South and 9° West would have a UTM coordinate of Zone 29, 500000 meters E, 4461369 meters N (remember that northing in the Southern Hemisphere is measured from 10,000,000 meters south of the equator - see Figures 2b-4 and 2b-5).
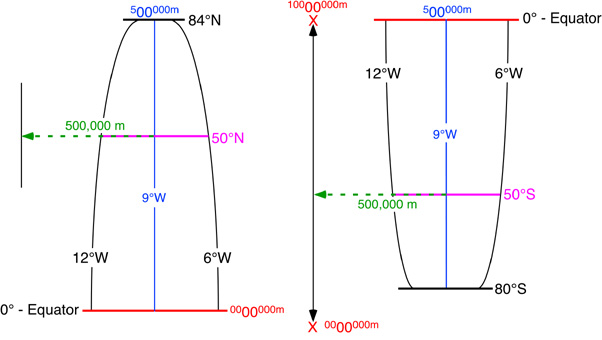
Figure 2b-4: The following illustration describes the characteristics of the UTM zone "29" found between 12 to 6° West longitude. Note that the zone has been split into two halves. The half on the left represents the area found in the Northern Hemisphere. The Southern Hemisphere is located on the right. The blue line represents the central meridian for this zone. Locations measurements for this zone are calculated relative to a false origin. In the Northern Hemisphere, this origin is located 500,000 meters west of the equator. The Southern Hemisphere UTM measurements are determined relative to a origin located at 10,000,000 meters south and 500,000 meters west of the equator and central meridian, respectively. |
The UTM system has been modified to make measurements less confusing. In this modification, the six degree wide zones are divided into smaller pieces or quadrilaterals that are eight degrees of latitude tall. Each of these rows is labeled, starting at 80° South, with the letters C to X consecutively with I and O being omitted (Figure 2b-5). The last row X differs from the other rows and extends from 72 to 84° North latitude (twelve degrees tall). Each of the quadrilaterals or grid zones are identified by their number/letter designation. In total, 1200 quadrilaterals are defined in the UTM system.
The quadrilateral system allows us to further define location using the UTM system. For the location 50° North and 9° West, the UTM coordinate can now be expressed as Grid Zone 29U, 500000 meters E, 5538630 meters N.
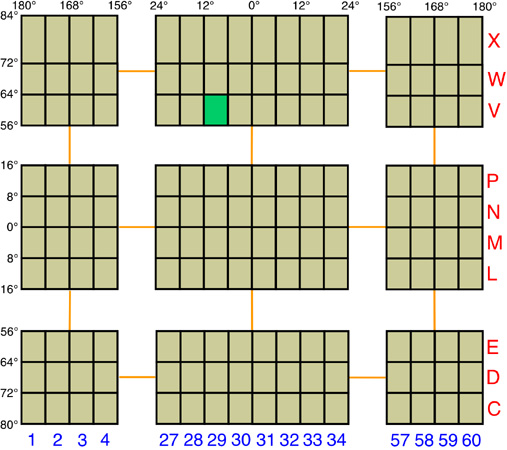
Figure 2b-5: The UTM system also uses a grid system to break the Earth up into 1200 quadrilaterals. To keep the illustration manageable, most of these zones have been excluded. Designation of each quadrilaterals is accomplished with a number-letter system. Along the horizontal bottom, the six degree longitude wide zones are numbered, starting at 180° West longitude, from 1 to 60. The twenty vertical rows are assigned letters C to X with I and O excluded. The letter, C, begins at 80° South latitude. Note that the rows are 8 degrees of latitude wide, except for the last row X which is 12 degrees wide. According to the reference system, the bright green quadrilateral has the grid reference 29V (note that in this system west-east coordinate is given first, followed by the south-north coordinate). This grid zone is found between 56 and 64° North latitude and 6 and 12° West longitude. |
Each UTM quadrilateral is further subdivided into a number of 100,000 by 100,000 meter zones. These subdivisions are coded by a system of letter combinations where the same two-letter combination is not repeated within 18 degrees of latitude and longitude. Within each of the 100,000 meter squares one can specify location to one-meter accuracy using a 5 digit eastings and northings reference system.
The UTM grid system is displayed on all United States Geological Survey (USGS) and National Topographic Series (NTS) of Canada maps. On USGS 7.5-minute quadrangle maps (1:24,000 scale), 15-minute quadrangle maps (1:50,000, 1:62,500, and standard-edition 1:63,360 scales), and Canadian 1:50,000 maps the UTM grid lines are drawn at intervals of 1,000 meters, and are shown either with blue ticks at the edge of the map or by full blue grid lines. On USGS maps at 1:100,000 and 1:250,000 scale and Canadian 1:250,000 scale maps a full UTM grid is shown at intervals of 10,000 meters. Figure 2b-6 describes how the UTM grid system can be used to determine location on a 1:50,000 National Topographic Series of Canada map.
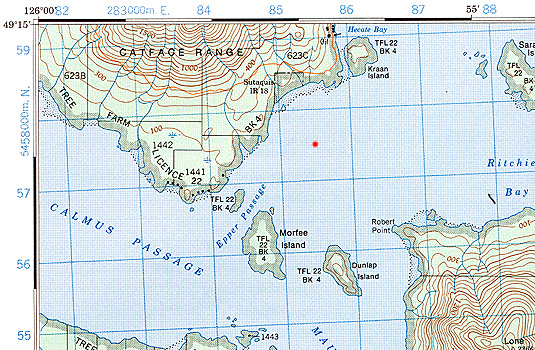
Figure 2b-6: The top left hand corner the "Tofino" 1:50,000 National Topographic Series of Canada map is shown above. The blue lines and associated numbers on the map margin are used to determine location by way of the UTM grid system. Abbreviated UTM 1,000-meter values or principle digits are shown by numbers on the map margin that vary from 0 to 100 (100 is actually given the value 00). In each of the corners of the map, two of the principle digits are expressed in their full UTM coordinate form. On the image we can see 283000 m E. and 5458000 m N. The red dot is found in the center of the grid defined by principle numbers 85 to 86 easting and 57 to 58 northing. A more complete UTM grid reference for this location would be 285500 m E. and 5457500 m N. Information found on the map margin also tells us (not shown) that the area displayed is in Grid Zone 10U and the 100,000 m squares BK and CK are located on this map. |
Distance on Maps
In section 2a, w e have learned that depicting the Earth's three-dimensional surface on a two-dimensional map creates a number of distortions that involve distance, area, and direction. It is possible to create maps that are somewhat equidistance. However, even these types of maps have some form of distance distortion. Equidistance maps can only control distortion along either lines of latitude or lines of longitude. Distance is often correct on equidistance maps only in the direction of latitude.
On a map that has a large scale, 1:125,000 or larger, distance distortion is usually insignificant. An example of a large-scale map is a standard topographic map. On these maps measuring straight line distance is simple. Distance is first measured on the map using a ruler. This measurement is then converted into a real world distance using the map's scale. For example, if we measured a distance of 10 centimeters on a map that had a scale of 1:10,000, we would multiply 10 (distance) by 10,000 (scale). Thus, the actual distance in the real world would be 100,000 centimeters.
Measuring distance along map features that are not straight is a little more difficult. One technique that can be employed for this task is to use a number of straight-line segments. The accuracy of this method is dependent on the number of straight-line segments used (Figure 2b-7). Another method for measuring curvilinear map distances is to use a mechanical device called an opisometer. This device uses a small rotating wheel that records the distance traveled. The recorded distance is measured by this device either in centimeters or inches.
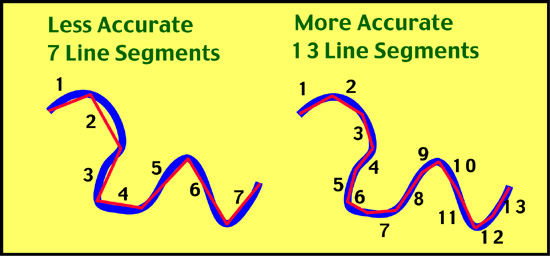
Figure 2b-7: Measurement of distance on a map feature using straight-line segments. |
Direction on Maps
Like distance, direction is difficult to measure on maps because of the distortion produced by projection systems. However, this distortion is quite small on maps with scales larger than 1:125,000. Direction is usually measured relative to the location of North or South Pole. Directions determined from these locations are said to be relative to True North or True South. The magnetic poles can also be used to measure direction. However, these points on the Earth are located in spatially different spots from the geographic North and South Pole. The North Magnetic Pole is located at 78.3° North, 104.0° West near Ellef Ringnes Island, Canada. In the Southern Hemisphere, the South Magnetic Pole is located in Commonwealth Day, Antarctica and has a geographical location of 65° South, 139° East. The magnetic poles are also not fixed overtime and shift their spatial position overtime.
Topographic maps normally have a declination diagram drawn on them (Figure 2b-8). On Northern Hemisphere maps, declination diagrams describe the angular difference between Magnetic North and True North. On the map, the angle of True North is parallel to the depicted lines of longitude. Declination diagrams also show the direction of Grid North. Grid North is an angle that is parallel to the easting lines found on the Universal Transverse Mercator (UTM) grid system (Figure 2b-8).
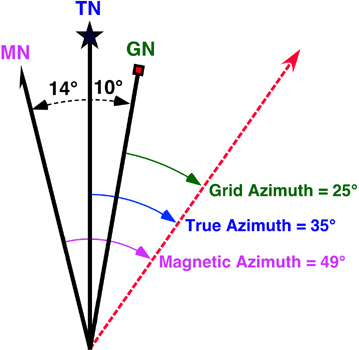
Figure 2b-8: This declination diagram describes the angular difference between Grid, True, and Magnetic North. This illustration also shows how angles are measured relative grid, true, and magnetic azimuth. |
In the field, the direction of features is often determined by a magnetic compass which measures angles relative to Magnetic North. Using the declination diagram found on a map, individuals can convert their field measures of magnetic direction into directions that are relative to either Grid or True North. Compass directions can be described by using either the azimuth system or the bearing system. The azimuth system calculates direction in degrees of a full circle. A full circle has 360 degrees (Figure 2b-9). In the azimuth system, north has a direction of either the 0 or 360°. East and west have an azimuth of 90° and 270°, respectively. Due south has an azimuth of 180°.
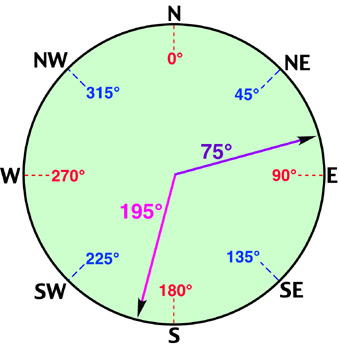
Figure 2b-9: Azimuth system for measuring direction is based on the 360 degrees found in a full circle. The illustration shows the angles associated with the major cardinal points of the compass. Note that angles are determined clockwise from north. |
The bearing system divides direction into four quadrants of 90 degrees. In this system, north and south are the dominant directions. Measurements are determined in degrees from one of these directions. The measurement of two angles based on this system are described in Figure 2b-10.
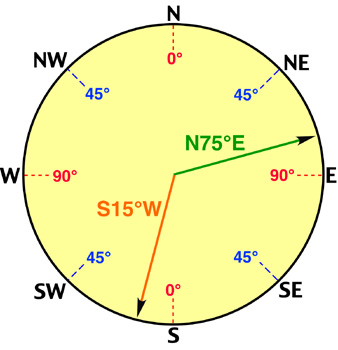
Figure 2b-10: The bearing system uses four quadrants of 90 degrees to measure direction. The illustration shows two direction measurements. These measurements are made relative to either north or south. North and south are given the measurement 0 degrees. East and west have a value of 90 degrees. The first measurement (green) is found in the north - east quadrant. As a result, its measurement is north 75 degrees to the east or N75°E. The first measurement (orange) is found in the south - west quadrant. Its measurement is south 15 degrees to the west or S15°W. |
Global Positioning Systems
Determination of location in field conditions was once a difficult task. In most cases, it required the use of a topographic map and landscape features to estimate location. However, technology has now made this task very simple. Global Positioning Systems (GPS) can calculate one's location to an accuracy of about 30-meters (Figure 2b-11). These systems consist of two parts: a GPS receiver and a network of many satellites. Radio transmissions from the satellites are broadcasted continually. The GPS receiver picks up these broadcasts and through triangulation calculates the altitude and spatial position of the receiving unit. A minimum of three satellite is required for triangulation.

Figure 2b-11: Handheld Global Positioning Systems (GPS). GPS receivers can determine latitude, longitude, and elevation anywhere on or above the Earth's surface from signals transmitted by a number of satellites. These units can also be used to determine direction, distance traveled, and determine routes of travel in field situations. |